①圧傾度力、コリオリ力、摩擦力が釣り合って海上を進んできた風が、同じ緯度の陸上に吹き込んだとき、海岸線付近で風速が変化し、収束が生じることがある。
収束とは、ある場所に空気が集まってくる状態のことです。陸上は海上に比べて摩擦力が大きくなるため、海岸線付近で風速が 弱まり 、収束が生じる ことがあります。したがって、答えは 正 です。
②地表付近に水平収束がある場は、一般的に下降流域である。 🟢
水平収束で集まった地表付近の空気は、地面より下へ移動できないので、上昇流 となって上空へ移動します。例えば、風が吹き込む低気圧の中心では 上昇流 が生じ、上空では雲が発生します。
逆に、地上で 発散 がある場合には 下降流 が生じます。したがって、地表付近に水平収束がある場は、一般的に「下降流域」ではなく「 上昇流域 」となりますので、答えは 誤 です。
③渦度とは、大気の回転方向と回転の速さを表す物理量であり、回転が速いほど、渦度が大きいと表現する。
渦度(読:うずど)とは、大気の回転方向と回転の速さを表す物理量です。
大気の流れはまっすぐ進むものだけではなく、回転しているものもあります。
この回転している状態を表すものが渦度です。
また、回転方向には、反時計回り(正)と時計回り(負)があり、回転が 速い ほど、渦度が 大きい と表現します。したがって、答えは 正 です。
④相対渦度の鉛直成分は、東西方向での南北風の変化と、南北方向での東西風の変化から求めることができる。
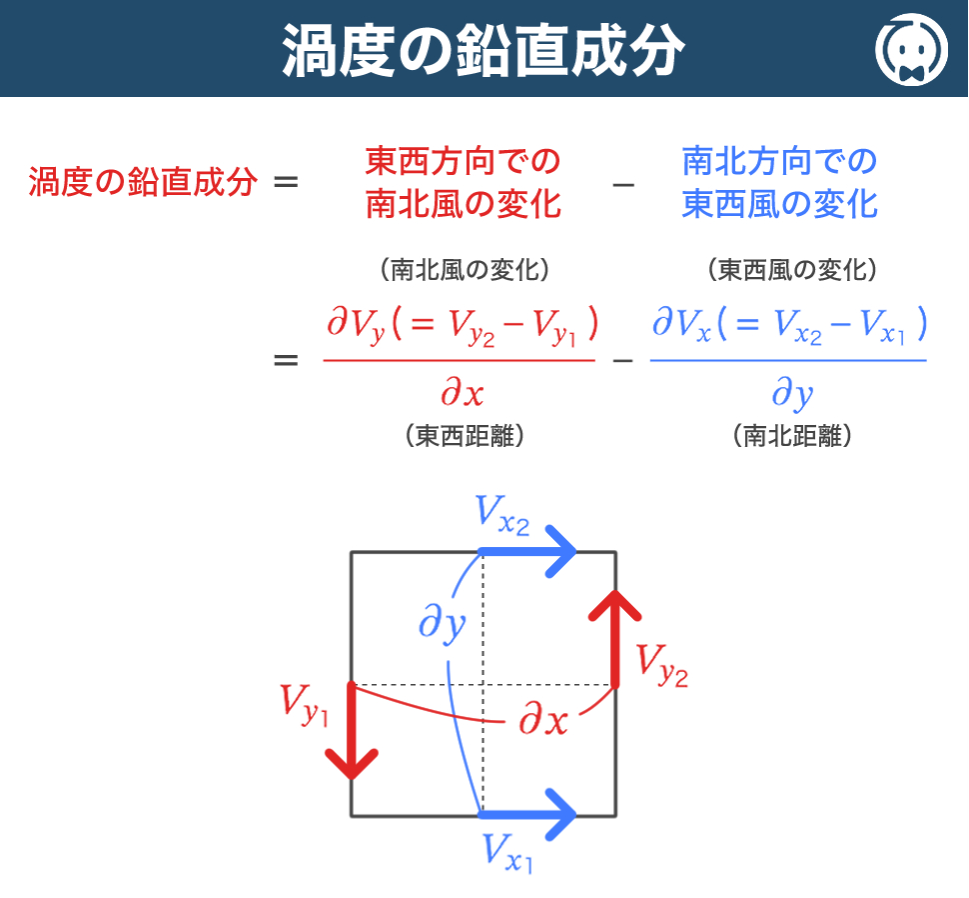
① 東西方向での南北風の変化 と、② 南北方向での東西風の変化 から、相対渦度の鉛直成分を求めることができますので、答えは 正 です。
⑤北半球の水平面内に図のような一辺の長さが2kmの正方形の領域(a)~(c)があり、各辺上では、辺に沿って図に示す強さの成分を持った風が吹いている。領域(a)~(c)内の渦度の鉛直成分の値を A ~ C とするとき、これらの大小関係は、B < A < C となる。ただし、渦度の鉛直成分は各領域内で一様とする。
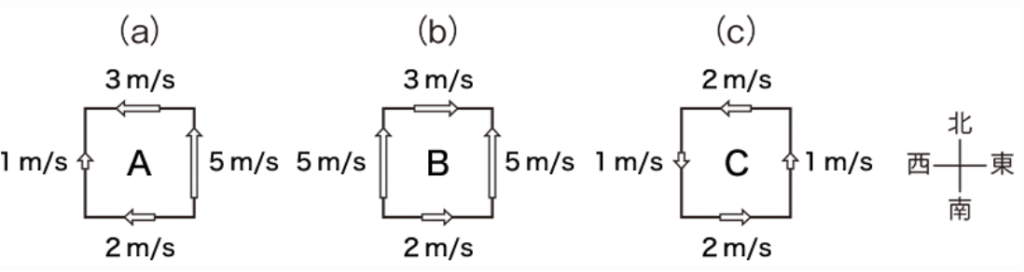
問題④に示した渦度の鉛直成分の式に当てはめてみると、渦度の鉛直成分の大小関係は B < A < C となりますので、答えは 正 です。

問題④に示した渦度の鉛直成分の式に当てはめてみると、渦度の鉛直成分の大小関係は B < A < C となりますので、答えは 正 です。
⑥下図の矢印の向きが水平面内の風向を表し、矢印の長さが風速を表しているとすると、北半球では、渦度は正である。ただし、反時計回りの回転を正の渦度、時計回りの回転を負の渦度とする。
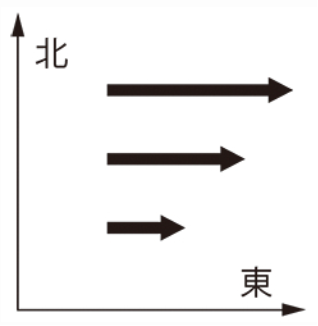
本問では、北に行くほど風速が 大きく なっていますので、渦度は 負 となります。したがって、渦度は「正」ではなく「 負 」ですので、答えは 誤 です。
⑦地球大気の渦度の鉛直成分は、地球の自転によって生じるものと大気が地球に対して相対的に運動することによって生じるものに分けることができ、大気が地球に対して相対的に運動することによって生じるものを惑星渦度という。
地球の自転によって生じる渦度を 惑星渦度 といい、大気が地球に対して相対的に運動することによって生じる渦度を 相対渦度 といいます。また、惑星渦度は、コリオリパラメータ f と同じ物理量で、地球の自転角速度を Ω 、緯度を φ とすると、以下の式で定義されます。f = 2Ωsinφ
したがって、大気が地球に対して相対的に運動することによって生じる渦度は「惑星渦度」ではなく「 相対渦度 」ですので、答えは 誤 です。
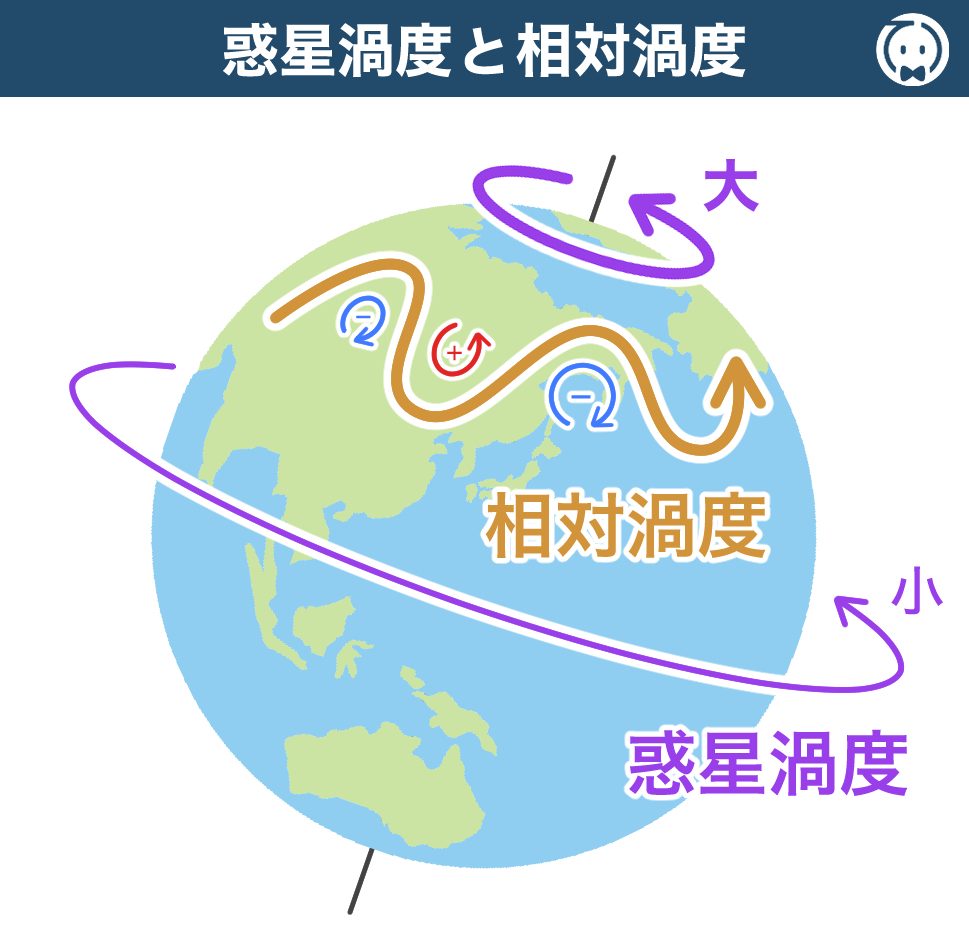
⑧北半球では、惑星渦度は正の値で、その大きさは北極点で最大である。
惑星渦度 f は、2Ωsinφ(Ω:地球の自転角速度、φ:緯度)で定義されます。
緯度 φ は、北半球では 正 の値をとるので、惑星渦度 f は 正 の値となります。
また、惑星渦度 f の大きさは、緯度が高くなるほど大きくなり、北極点(φ = 90°)で 最大 となります。したがって、答えは 正 です。
⑨惑星渦度と相対渦度の和を絶対渦度といい、一般に、地球上の空気塊の絶対渦度は、粘性や水平収束・発散がなければ近似的に保存される性質がある。
これを、絶対渦度保存則 といい、
絶対渦度 = 惑星渦度 + 相対渦度
の式で表されます。 したがって、答えは 正 です。
⑩鉛直p速度は、ある空気塊の気圧の時間変化率を表し、上昇流域では正の値となる。
鉛直p速度 ω は 気圧の時間変化率を表す物理量で、以下の式で定義されます。したがって、鉛直p速度は、ある空気塊の気圧の時間変化率を表し、上昇流域では「正」ではなく「負」の値となりますので、答えは 誤 です。
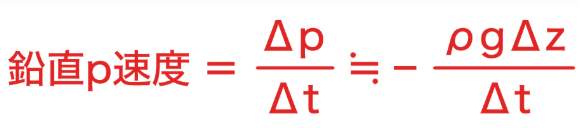
⑪850hPa 等圧面の高度が6時間で1500m から1560m に上昇した。空気の密度を 1kgm-3 、重力加速度を 10ms-2 とすると、このときの鉛直p速度は、1hPa/h となる。ただし、1hPa = 100kgm-1s-2 とする。
この式に問題文の数値を⑩の式当てはめて計算すると
答えは「1hPa/h」の下降流ではなく「 −1hPa/h 」の上昇流となりますので、答えは 誤 です。



コメント
> 一般 大気の力学:大気の流れと渦度 11問題
正誤問題は、なんか読み進めて練習していけば当たりそうですか?ナイナイ
パス