I13大気と放射13問１周目

①地球大気は、太陽放射に対して近似的に黒体とみなせることから、その吸収量の計算にはプランクの法則を適用できる。🟢

プランクの法則は、黒体が放射するエネルギー量を計算するのであって、吸収するエネルギー量を計算する法則ではありません。地球大気は、太陽放射に対して近似的にも黒体とみなすことはできず、その吸収量の計算にプランクの法則は適用できませんので、答えは誤です。

②波長0.3μm以下の紫外線がほとんど地表面に到達していないのは、成層圏界面に達する前に、酸素分子及びオゾンによってほぼ吸収されるからである。🟢

太陽放射のうち波長が0.3μm以下の紫外線は、「成層圏界面」ではなく、「対流圏界面」に到達するまでに酸素分子やオゾンによってほぼ吸収されてしまい、ほとんど地表面には到達していませんので、答えは誤です。

③地球大気において地球放射を最も多く吸収している気体は二酸化炭素で、次がメタンである。🟢

最も地球放射を吸収している気体は「二酸化炭素」ではなく「水蒸気 ( H₂O )」ですので、答えは誤です。

④大気上端で放射平衡が成り立っている場合、大気上端における上向き地球放射量は、入射太陽放射量とアルベドの積に等しい🟢

大気上端で放射平衡が減り立っている場合、大気上端における上向きの地球放射量（Z）は、入射する太陽放射量（X）とアルベド（A）との積ではなく、入射する太陽放射量（X）と（1 － A ）との積に等しいので、答えは誤です。

⑤地球に入射する太陽放射量と、地球が反射した太陽放射量の比をアルベドといい、地球に入射してきた太陽放射の約30%が地表面の反射によって宇宙空間に戻っている。🟢

地球に入射してきた太陽放射の約30%が「地表面の反射」だけでなく「地表面の反射と、大気中の気体分子･エーロゾル･雲による反射と散乱」によって宇宙空間に戻っていますので、答えは誤です。

⑥黒体の表面から単位面積、単位時間あたりに放射される電磁波のエネルギーは、その黒体の絶対温度の４乗に比例する。🟢

この関係をステファン・ボルツマンの法則といい、以下の式で表されます。
I＝σT⁴
（ I：単位面積から単位時間に放射されるエネルギー、σ：ステファン･ボルツマン定数、T：黒体の絶対温度）
したがって、黒体の表面から単位面積、単位時間あたりに放射される電磁波のエネルギーは、その黒体の絶対温度の４乗に比例しますので、答えは正です。

⑦黒体の単位波長あたりの放射強度が最大となる波長 (λm) は、黒体の表面温度 (T) に反比例する。🟢

この関係をウィーンの変位則といい、以下の式で表されます。
λm ＝ 2897/T
（ λm：黒体の単位波長あたりの放射強度が最大となる波長、T：黒体の表面温度）
したがって、2897は定数なので、分母の黒体の表面温度 (T) の値が大きくなると、黒体の単位波長あたりの放射強度が最大となる波長 (λm) は小さくなる反比例の関係にありますので、答えは正です。

⑧大気中の粒子の半径が電磁波の波長よりも非常に小さい場合の散乱はレイリー散乱であり、日中の晴れた空が青く見えるのはこのためである。

大気中の粒子の半径が電磁波の波長よりも非常に小さい場合の散乱はレイリー散乱であり、日中の晴れた空が青く見えるのはこのためですので、答えは正です。

⑨ミー散乱では、散乱の強さは電磁波の波長にあまり依存しない。雲が白く見えるのはこのためである。

ミー散乱では、散乱の強さは電磁波の波長にあまり依存せず、雲が白く見えるのはこのためですので、答えは正です。

⑩波長11μmを中心とする８〜12μmの赤外線領域に、大気の窓と呼ばれる地球放射に対する大気による吸収が強い波長帯がある。

波長11μmを中心とする８〜12μmの赤外線領域に、大気の窓と呼ばれる地球放射に対する大気による吸収が「強い」ではなく「弱い」波長帯がありますので、答えは誤です。

⑪図は地球（地球大気と地球表層）について年平均したエネルギー収支を表し、大気上端、大気内部、地表面の間でやりとりされる、短波放射･長波放射の強さ、乱流による顕熱や潜熱の輸送量が示されている。また、折れた矢印は地表面または大気内部における短波放射の反射の強さを表しており、大気上端、大気内部、地表面のそれぞれにおいてエネルギー収支は釣り合っている。このとき、外向き短波放射の合計から、地表面で反射される短波放射 A は 30 Wm-2 となり、入射短波放射の収支から、地表面で吸収される短波放射 B は 174 Wm-2 となる。

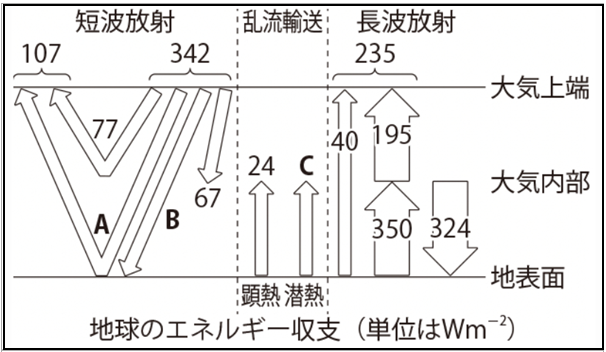
大気上端から入ってくる短波放射の放射量は 342 で、その内訳は 77 と A と B と 67 を足したものです。つまり、
342 ＝ 77＋A＋B＋67・・・（１）
という関係が成り立ちます。
また、大気上端から出ていく短波放射の合計は 107 なので、
107 ＝ 77＋A・・・（２）
という関係が成り立ちます。
（１）、（２）式より、A は 30 Wm-2 となります。
また、入射する短波放射の収支は
342−107 ＝ 235
なので、
235 ＝ B＋67
より、Bは 168 Wm-2 となります。
したがって、地表面で反射される短波放射Aは「 30 Wm-2 」で正しいですが、地表面で吸収される短波放射Bは「174 Wm-2」ではなく「 168 Wm-2 」となりますので、答えは誤です。
大気内部への入射量は 67 と 24 と C と 350 です。
大気内部を通過する 40 は、内部への入射量には算入しません。
一方、大気内部からの放射量は 195 と 324 です。
大気内部への入射量と大気内部からの放射量は釣り合っていますので、
67＋24＋C＋350 ＝ 195＋324
より、C は 78 Wm-2 となりますので、答えは正です。

⑫図（⑪と同じ)は地球（地球大気と地球表層）について年平均したエネルギー収支を表し、大気上端、大気内部、地表面の間でやりとりされる、短波放射･長波放射の強さ、乱流による顕熱や潜熱の輸送量が示されている。また、折れた矢印は地表面または大気内部における短波放射の反射の強さを表しており、大気上端、大気内部、地表面のそれぞれにおいてエネルギー収支は釣り合っている。このとき、地表面または大気内部におけるエネルギー収支から潜熱 C は 78 Wm-2 と見積もることができる。

地球が受け取る太陽放射量は、低緯度ではほぼ垂直に入射するため大きいですが、高緯度では入射角が小さいため、同じ面積に対して受け取るエネルギーは小さくなります。
一方、地球から放出される長波放射は、地表の温度に依存するものの、年平均では放射量に大きな緯度差はありません。
そのため、北緯80°のような高緯度域では、太陽から受け取る短波放射は非常に小さくなりますが、長波放射はほとんど変わりません。
結果として、緯度別に年平均すると、北緯80°において受け取る太陽放射量は、長波放射量よりも「大きい」ではなく「小さい」ので、答えは誤です。

⑬緯度別に年平均すると、北緯80°において受け取る太陽放射量は、長波放射量よりも大きい。

地球が受け取る太陽放射量は、低緯度ではほぼ垂直に入射するため大きいですが、高緯度では入射角が小さいため、同じ面積に対して受け取るエネルギーは小さくなります。

一方、地球から放出される長波放射は、地表の温度に依存するものの、年平均では放射量に大きな緯度差はありません。そのため、北緯80°のような高緯度域では、太陽から受け取る短波放射は非常に小さくなりますが、長波放射はほとんど変わりません。結果として、緯度別に年平均すると、北緯80°において受け取る太陽放射量は、長波放射量よりも「大きい」ではなく「小さい」ので、答えは誤です。