ブライアスコア
ブライアスコアは値が小さい (誤差が少ない)ほど精度が高い
①ブライアスコアは、確率予報の精度を評価する指標で、値が1に近いほど予報の精度が高い。
ブライアスコア とは、気象予報における確率予報の精度を評価する指標で、予報の正確さを数値化したものです。
具体的な計算手順は以下のとおりです。
① 予報値(%)を0~1の小数に変換する(例:30% → 0.3)
② 実況値は「 降水あり=1」「 降水なし=0」とする
③ それぞれの回で「 予報値-実況値 」の差を求める
④ その差を2乗 する
⑤ すべての回について2乗値を 合計 し、回数で割る
ブライアスコアは、値が0に近い ほど 予報が正確 であり、1に近い ほど 誤差が大きい ことを示します。
つまり、ブライアスコアは値が 小さい (誤差が少ない)ほど 精度が高い ということです。
したがって、ブライアスコアは、確率予報の精度を評価する指標で、値が1に近いほど予報の精度が「高い」ではなく「 低い 」ので、答えは 誤 です。

②ブライアスコアは現象の発生頻度(気候学的出現率)に影響を受けるため、出現率が大きく異なる現象同士の精度比較には適さない。
ブライアスコア とは、気象予報における確率予報の精度を評価する指標で、予報の正確さを数値化したものです。
ブライアスコアは、値が 小さい ほど予報精度が 高い ことを示しますが、現象の発生頻度(気候学的出現率)の影響を 強く受ける という点に注意が必要です。
例えば、ある現象(降水や雷など)の発生頻度が 非常に低い 場合、その現象がほとんど起こらない地域や期間では、常に「 発生しない 」と予報するだけでブライアスコアは 低く なります。
逆に、発生頻度が 高い 現象については、同じ予報手法でもブライアスコアが 高く なりやすくなります。
つまり、現象ごとに出現率が異なると、同じ予報手法であってもブライアスコアの値が変わってしまい、単純な数値比較だけでは予報技術そのものの優劣を 正しく評価できません。
したがって、ブライアスコアは現象の発生頻度(気候学的出現率)に影響を受けるため、出現率が大きく異なる現象同士の精度比較には適さないので、答えは 正 です。
⑦降水確率予報の精度が高いのはX社である。

ブライアスコア(BS:Brier Score) とは、確率で予測する予報(例:降水確率)と実際の結果の誤差を評価する指標です。簡単に言うと、降水確率のような、確率予報の精度を評価する指標です。
ブライアスコアは下式で定義され、確率予報値と実況値の差の二乗を平均して求めます。(N:標本数、pi:確率予報値(0〜1(例:予報確率80%=0.8))、ai:実況値(現象ありで1、現象なしで0))
ブライアスコアは 0〜1 までの値をとり、0に近い ほど予報精度が 良く 、1に近い ほど予報精度が 悪い 、と評価されます。
降水確率予報 という、確率予報の精度を検証するためには、ブライアスコア を使用します。
問題の表を見てみると、Y社 の方がブライアスコアが 小さい ので、Y社の方が降水確率予報の予報精度が 良い ことが分かります。
したがって、降水確率予報の精度が高いのは「X社」ではなく「 Y社 」ですので、答えは 誤 です。

スレットスコア
スレットスコア は、主に発生頻度が少ない現象の予報精度を評価する指標
③スレットスコアは、主に発生頻度が少ない現象の予報精度を評価する指標で、値が0に近いほど予報精度が高い。
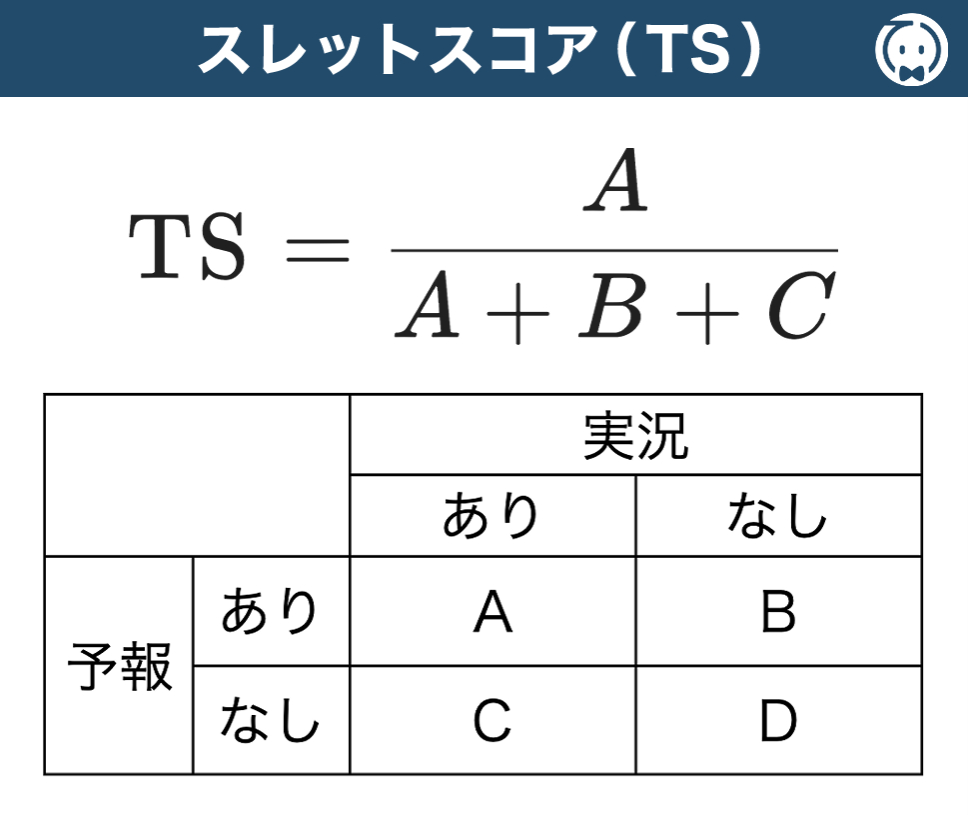
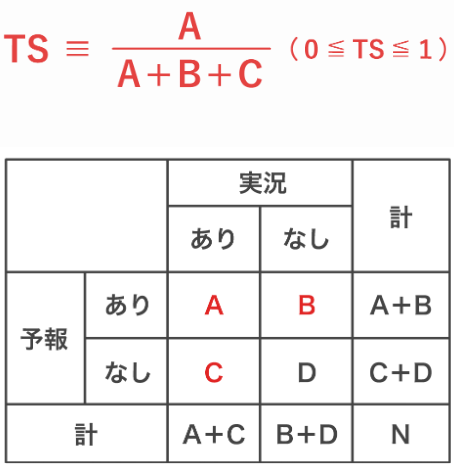
スレットスコア とは、主に発生頻度が少ない現象の予報精度を評価する指標です。
A:予報あり・実況あり(現象が発生すると予報し、実際に発生した回数=的中)
B:予報あり・実況なし(現象が発生すると予報したが、実際には発生しなかった回数=空振り)
C:予報なし・実況あり(現象が発生しないと予報したが、実際には発生した回数=見逃し)
このとき、D(予報なし・実況なし)は分母に含めません。
つまり、当たり前に外れるケース(例:雨が降らないと予報し、実際に降らなかった)を評価から除外することで、発生頻度が低い現象 に対する予報精度を正しく評価できるのです。
スレットスコアの値は0~1の範囲で、0に近い ほど 誤差が大きく、1に近い ほど 予報が正確 であることを示します。
したがって、スレットスコアは、主に発生頻度が少ない現象の予報精度を評価する指標で、値が0に近いほど予報精度が「高い」ではなく「 低い 」ので、答えは 誤 です。
バイアススコア
バイアススコアが1の時、予報の回数と実際の発生回数が一致しており、予報に 偏りがない 状態を表します。
④バイアススコアは、予報の偏りを示す指標で、値が1より大きければ見逃しが多く、1より小さければ空振りが多い。
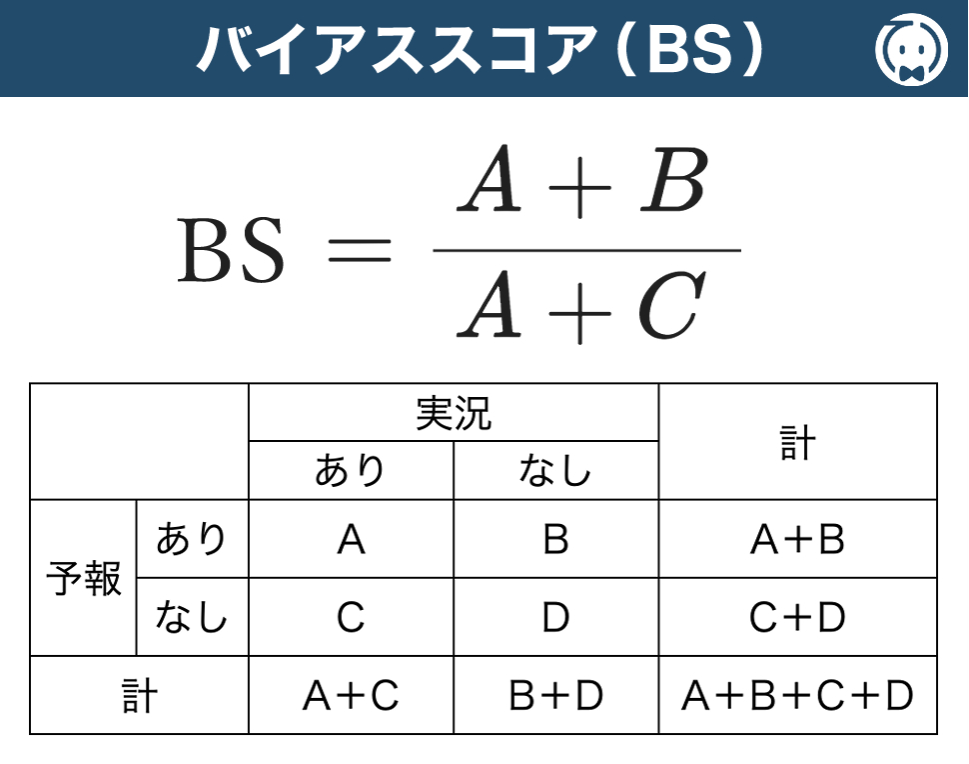
バイアススコア とは、予報の偏りを示す指標で、予報で「現象あり」とした回数を実際に「現象あり」となった回数で割って求めます。
分子:予報で「現象あり」と予測した
回数(例:雨が降ると予報した回数)
分母:実際に「現象あり」となった回数(例:実際に雨が降った回数)
バイアススコアが1の時、予報の回数と実際の発生回数が一致しており、予報に 偏りがない 状態を表します。
また、バイアススコアが1より大きい ほど、予報で「現象あり」とした回数が実際より 多く、空振りが多い、つまり現象の発生を 過大評価 していることを表します。
逆に、バイアススコアが1より小さい ほど、予報で「現象あり」とした回数が実際より 少なく、見逃しが多い、つまり現象の発生を 過小評価 していることを表します。
したがって、バイアススコアは、予報の偏りを示す指標で、値が1より大きければ「見逃し」ではなく「 空振り 」が多く、1より小さければ「空振り」ではなく「 見逃し 」が多いので、答えは 誤 です。
平均誤差と二乗平均平方根誤差
⑤翌日の最高気温の予報精度が高いのはX社である。

平均誤差(ME:Mean Error)とは、量的予報(例:気温、風速など)の誤差(=予報値−実況値)の 系統的な偏り を評価する指標です。簡単に言うと、実況値に比べて、予報値が全体的に大きいのか、小さいのかを判別する指標です。平均誤差は下式で定義され、予報値から実況値を差し引いた予報誤差の合計を、予報回数で割って求めます。(N:標本の数、xi:予報値、ai:実況値)
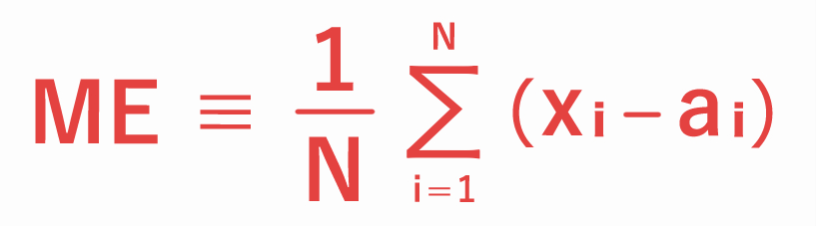
平均誤差は、値が プラス であれば予報が 過大 、マイナス であれば予報が 過小 であることを意味します。つまり、値が 0 のときは、平均的に見て、予報が 正にも負にも偏っていない ということです。しかし、正の誤差と負の誤差が 打ち消し合う 場合にも、値は 小さく なりますので、値が 小さい ほど予報精度が 良いわけではありません。
二乗平均平方根誤差(RMSE:Root Mean Square Error)とは、量的予報(例:気温、風速など)の誤差(=予報値−実況値)の 大きさ を評価する指標です。二乗平均平方根誤差は下式で定義され、予報値と実況値の誤差を二乗して平均し、その平方根を取って求めます。(N:標本の数、xi:予報値、ai:実況値)
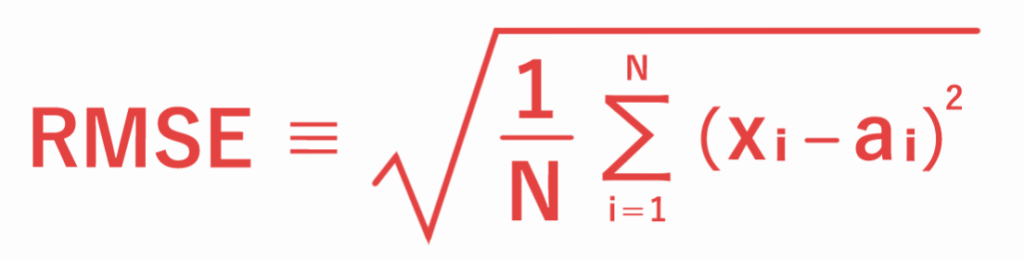
平均誤差 は、予報誤差の 偏り を評価していたのに対して、二乗平均平方根誤差 は、誤差を二乗していますので、誤差の正負(系統的な偏り)ではなく、誤差の 大きさ を評価します。
つまり、値が 0に近い ほど予報精度が 良く 、値が 大きい ほど誤差が 大きい ということです。
翌日の最高気温 という、量的予報の精度を検証するためには、二乗平均平方根誤差 を使用します。
問題の表を見てみると、Y社 の方が二乗平均平方根誤差が 小さい ので、Y社の方が翌日の最高気温の予報精度が 良い ことがわかります。
ちなみに、平均誤差は、X社とY社で符号の違いはあるものの、平均的にみると 偏りは同じ であり、予報精度が高いかどうかは 判断できません。
したがって、翌日の最高気温の予報精度が高いのは「X社」ではなく「 Y社 」ですので、答えは 誤 です。
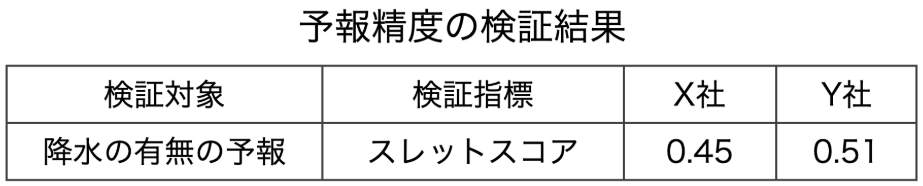
⑥降水の有無の予報精度が高いのはX社である。
スレットスコア(TS:Threat Score) とは、現象の発生頻度が少なく、発生を予想することの意味が大きい現象(例:太平洋側の降水、雷など)の予報精度を評価する指標です。
簡単に言うと、あまり発生しない現象をどれくらい予報できていたかを判別する指標です。
スレットスコアは下式で定義され、発生頻度が少ない現象をどれくらい正しく予報できたかを評価するために、事例数が多い「予報なし・実況なし」を除いた適中率で求めます。
スレットスコアは0〜1までの値をとり、1に近い ほど予報精度が 良く 、0に近い ほど予報精度が 悪い 、と評価されます。降水の有無の予報精度 という、現象の有無の精度を検証するためには、スレットスコア を使用します。
問題の表を見てみると、Y社 の方がスレットスコアが 大きい ので、Y社の方が降水の有無の予報精度が 良い ことが分かります。したがって、降水の有無の予報精度が高いのは「X社」ではなく「 Y社 」ですので、答えは 誤 です。
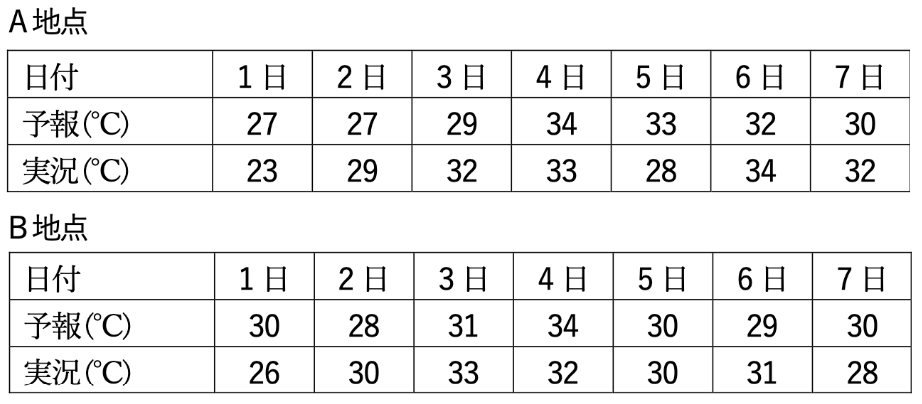
⑧表は、ある期間のA地点とB地点における日最高気温の予報と実況を示したものである。この期間の最高気温の予報について、系統的な偏りを平均誤差 (ME) により求めると、どちらの地点も正の偏りがある。
A地点
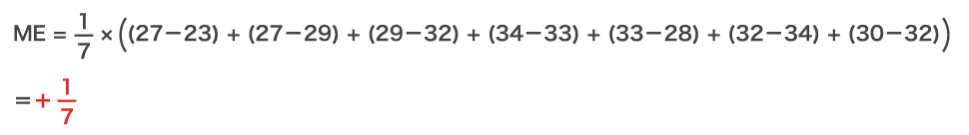
B地点 同様に計算して +2/7
したがって、平均誤差(ME)はどちらの地点も正であり、正の偏りがありますので、答えは 正 です。
⑨表は、ある期間のA地点とB地点における日最高気温の予報と実況を示したものである。この期間の最高気温の予報について、予報誤差の標準的な大きさを2乗平均平方根誤差 (RMSE) により求めると、B地点の方がA地点よりも予報誤差が大きい。
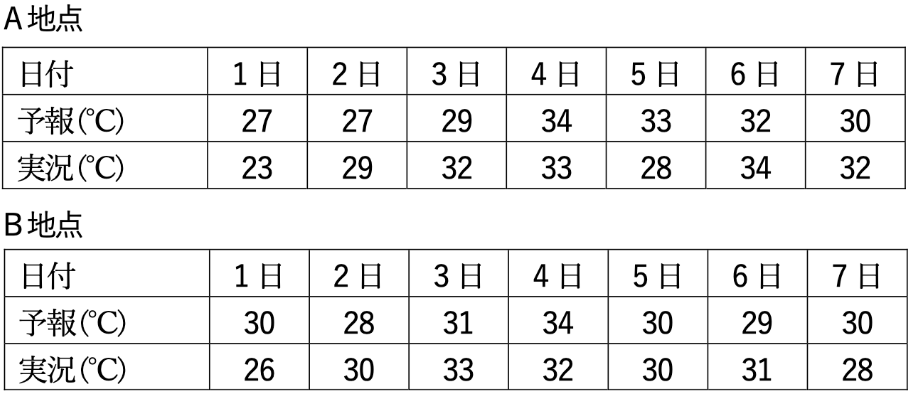
A地点
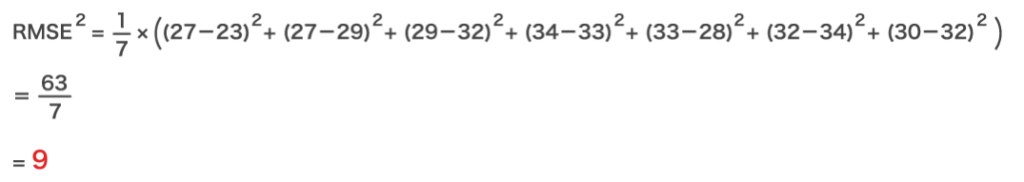
B地点 同様に計算して 5.1
したがって、2乗平均平方根誤差(RMSE)が大きいのは、「B地点」ではなく「A地点」
ですので、答えは 誤 です
見逃し率
⑩表は、ある期間のA地点とB地点における日最高気温の予報と実況を示したものである。この期間の真夏日の予報の見逃し率は、B地点の方がA地点よりも低い。(ただし、見逃し率は全予報数に対する割合とする。)
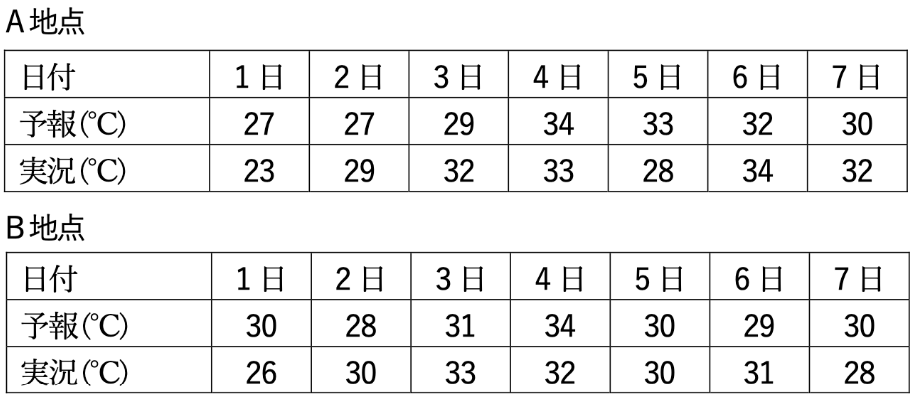
真夏日 とは、最高気温が30℃以上の日です。
見逃し率 とは、現象なしと予想したのに、現象が起きた日の割合のことです。
例えるなら、野球のバッターが、ボールだと思って見逃したのにストライクだった!みたいなかんじです。
なので、真夏日予報の見逃し率は、真夏日にならないと予報したのに、実況で真夏日になった日を、全体の標本数で割って求めます。
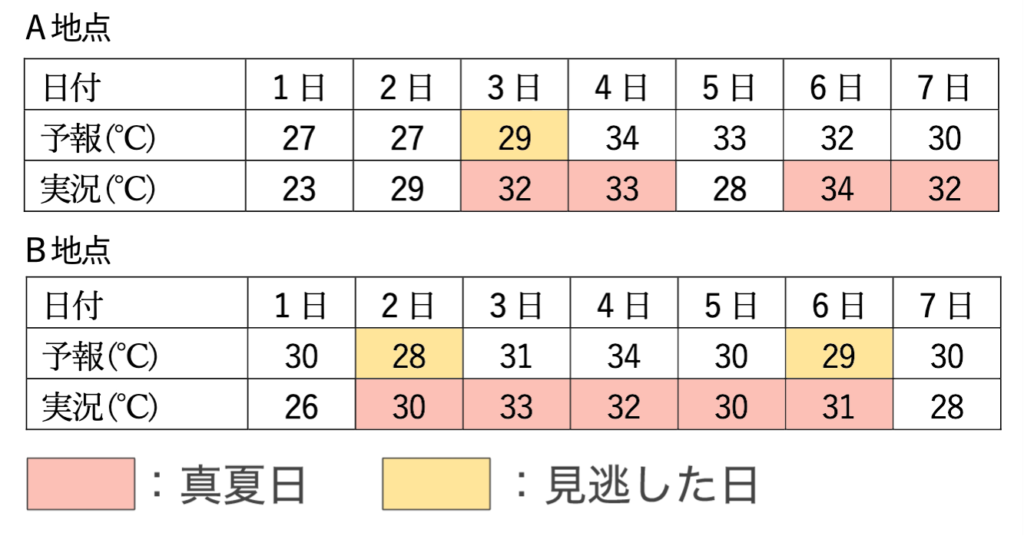
下図の赤色は実況で真夏日だった日、黄色は真夏日を見逃した日です。
上図から、真夏日の見逃し回数は、A地点は1回、B地点は2回なので、見逃し率はB地点の方が高くなります。
したがって、真夏日の予報の見逃し率は、B地点の方がA地点よりも「低い」ではなく「高い」ので、答えは 誤 です。




コメント