S5数値予報モデル(34)1周目

①観測点が密な陸上などの地域の観測データの情報は、データ同化と数値予報を繰り返すことにより、観測点が疎らな海上などの地域の解析値にも反映される。🟢

数値予報モデルを実行するためには、初期時刻の気温、風、水蒸気量など、３次元空間の全ての格子点に大気の物理量（初期値）を与えなければなりません。
この初期値の精度が数値予報の精度を左右するため、精度の高い初期値を作成することが重要です。
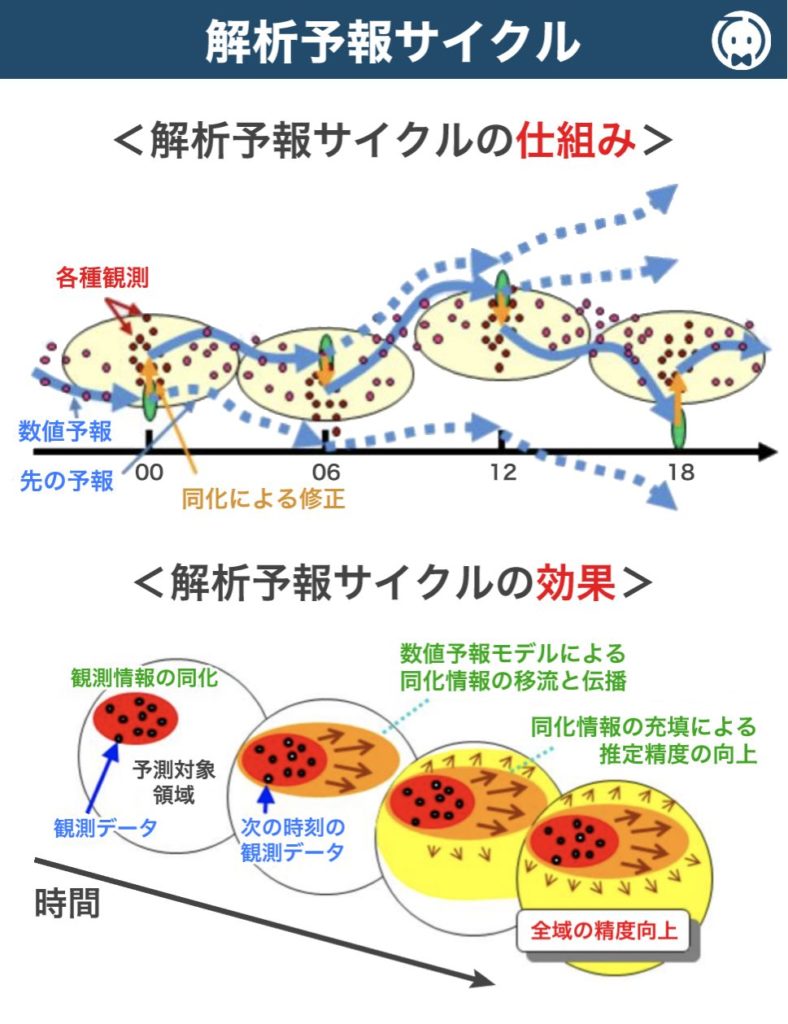
これを実現するために「解析予報サイクル」という手法が用いられます。
解析予報サイクルとは、数値予報モデルで得られた予報値を、次の解析（データ同化）の第一推定値として利用し、その解析値を初期値として次の予報を行うというサイクルを繰り返す手法です。
具体的には、ある時刻を初期時刻として予報を計算し、その予報結果を次の時刻の客観解析の第一推定値として利用します。その後、観測データを取り込んで修正（データ同化）し、新たな解析値を作成します。この解析値は次の予報の初期値となり、サイクルが繰り返されます。
このような解析予報サイクルを繰り返すことによって、観測データの影響は、数値予報モデルを介して周囲に広がっていきます。例えば、偏西風が卓越する中緯度では、大陸東岸で収集された観測データが、偏西風の影響で東海上の解析値に伝わり、その地域の数値予報の精度向上に寄与します。
このように、データ同化と数値予報を繰り返すことで、観測データの影響が広がり、観測点の少ない地域でも精度の高い解析値が得られる仕組みとなっています。
したがって、観測点が密な陸上などの地域の観測データの情報は、データ同化と数値予報を繰り返すことにより、観測点が疎らな海上などの地域の解析値にも反映されますので、答えは正です。

②プリミティブ方程式を用いる気象庁の全球モデルでは、大気の鉛直流は水平方向の運動方程式を使って予測した水平風から連続の式を用いて求めている。🟢

気象庁の全球モデルでは、水平スケールが鉛直スケールに比べて非常に大きい現象（総観規模現象）を扱うため、静力学平衡の近似を採用しています。
静力学平衡とは、鉛直方向の気圧傾度力と重力が釣り合っている状態を指し、この仮定を置くことで鉛直方向の運動方程式を計算する必要がなくなります。
この近似を前提とした方程式系を「プリミティブ方程式系」と呼び、それを用いた数値予報モデルを「プリミティブモデル」または「静力学モデル」といいます。
静力学平衡を仮定することで計算量を削減し、効率的に予測を行うことができますが、鉛直方向の運動方程式を使えないため、鉛直流（鉛直速度）を直接計算することはできません。
そこで、プリミティブモデルでは、水平風を水平方向の運動方程式で予測し、それを連続の式（空気の質量保存を表す方程式）と組み合わせることで鉛直流を間接的に求めています。
具体的には、連続の式が鉛直方向の質量移動を考慮することで、水平風の変化から鉛直流を計算します。
この方法は、水平スケールが十分に大きい場合に有効であり、全球モデルに適したアプローチです。
したがって、プリミティブ方程式を用いる気象庁の全球モデルでは、大気の鉛直流は水平方向の運動方程式を使って予測した水平風から連続の式を用いて求めていますので、答えは正です。

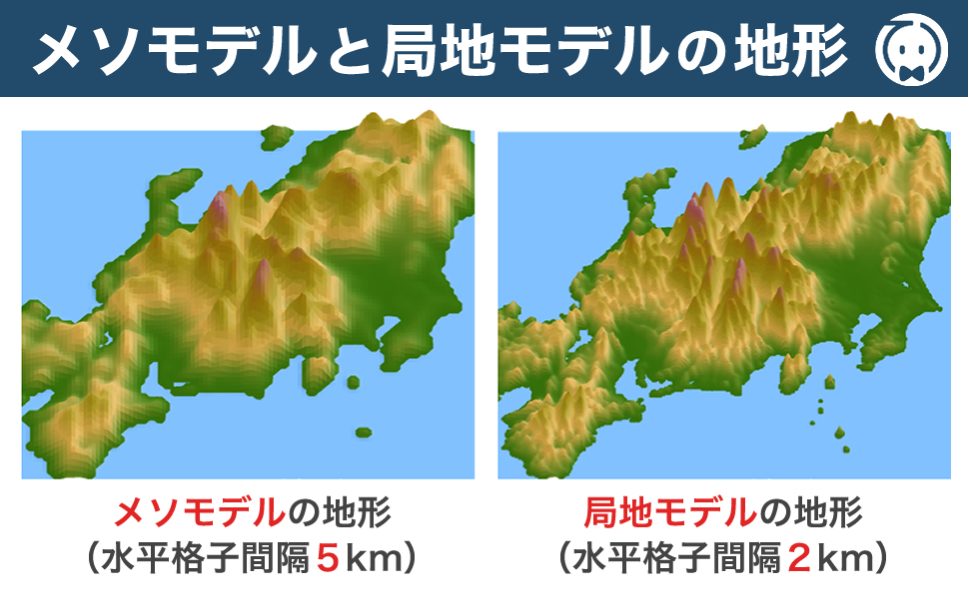
③気温・気圧などの気象要素は、水平方向の変化に比べて鉛直方向の変化の方が大きいので、気象庁のメソモデルや局地モデルでは鉛直方向の層の間隔を水平格子間隔より大きくしている。🟢

簡潔解説　気温や気圧などの気象要素は、鉛直方向の変化が水平方向より大きいため、数値予報モデルでは鉛直方向の層の間隔を細かく（＝小さく）設定しています。たとえば、メソモデルでは水平5kmに対して鉛直96層、局地モデルでは水平2kmに対して鉛直76層と、鉛直方向の解像度が高くなっています。また、大気の流れは上空ほど水平流が強く、下層ほど鉛直変化が大きいため、特に下層では層の間隔をさらに細かくしています。したがって、「鉛直方向の層の間隔を水平より大きくしている」という記述は誤りです。

④地球大気を扱う数値予報モデルでは、格子間隔より小さなスケールの現象によって生じる効果を、格子点における物理量を用いて近似的に評価しているので、実際の現象とは厳密に一致せず、誤差が生じる要因の一つとなっている。🟢

簡潔な解説： 数値予報モデルでは、大気などを格子状に分割して、各格子点で気温や風などを計算します。ただし、格子間隔より小さなスケールの現象（例：積雲など）は直接表現できません。そのため、そうした小さな現象の影響を格子点の物理量を使って近似的に評価します。これをパラメタリゼーションと呼びます。この近似には限界があるため、実際の現象とは完全には一致せず、誤差の原因にもなります。したがって、この記述は正しいです。

⑤仮に数値予報モデルが完全であり、初期値に含まれる誤差が微小であったとしても、大気の持つカオス的な性質により、予報時間が長くなるにしたがって予報誤差は急速に増大することが知られている。🟢

数値予報モデルには、連続的な気象現象を離散的な格子点で表現する際の誤差や、物理過程のパラメタリゼーションによる誤差があります。仮に、これらの誤差がない理想的なモデルを用いたとしても、初期値に誤差が含まれていた場合、予報時間が長くなるほど、大気の持つカオス的な性質により、誤差が急速に増大してしまいます。
例えば、メソスケール現象（積雲対流など）のように時空間スケールが小さく、非線形性が卓越する現象では、初期値に含まれる誤差が短時間のうちに増大し、予報の決定論的限界（＝予測可能な時間の限界）に達してしまいます。
したがって、仮に数値予報モデルが完全であり、初期値に含まれる誤差が微小であったとしても、大気の持つカオス的な性質により、予報時間が長くなるにしたがって予報誤差は急速に増大しますので、答えは正です。

⑥数値予報モデルにおいて、「雲による長波放射にともなう加熱量・冷却量」は、パラメタリゼーションによって計算される。🔵

パラメタリゼーションとは、数値予報モデルの格子点間隔以下のスケールの現象による効果の見積もりのことです。つまり、数値予報モデルで計算される物理量が、パラメタリゼーションによって計算されるかどうかは、それに関わる現象が数値予報モデルの格子点間隔で直接表現できるかどうか、という点から判断できます。
雲による長波放射は、大気や地表面に吸収されてそれらを加熱し、それに伴って雲は熱を失うので冷却されます。個々の雲の水平スケールは、気象庁の数値予報モデルの格子間隔より小さいことが多いので、雲からの長波放射やそれに伴う加熱量・冷却量を数値予報モデルで直接表現することは困難です。
したがって、雲による長波放射にともなう大気の加熱量・冷却量は、パラメタリゼーションによって計算されますので、答えは正です。

簡潔な解説： 雲による長波放射は、大気や地表を加熱し、雲自身は冷却される現象です。でも、雲は格子間隔より小さいスケールのことが多く、数値予報モデルでは直接表現できません。そのため、こうした効果はパラメタリゼーションによって近似的に計算されます。よって、この記述は正しいです。

⑦数値予報モデルにおいて、「コリオリ力による風の変化量」は、パラメタリゼーションによって計算される。

パラメタリゼーションとは、数値予報モデルの格子点間隔以下のスケールの現象による効果の見積もりのことです。つまり、数値予報モデルで計算される物理量が、パラメタリゼーションによって計算されるかどうかは、それに関わる現象が数値予報モデルの格子点間隔で直接表現できるかどうか、という点から判断できます。コリオリ力は、水平スケールが大きい現象ほど、その効果が大きくなります。
つまり、数値予報モデルの格子間隔で表現される風に働くコリオリ力は、その格子間隔で表現される風から計算できるということです。
したがって、コリオリ力による風の変化量は、パラメタリゼーションで計算する必要はありませんので、答えは誤です。

簡潔な解説： コリオリ力は、地球の自転によって生じる力で、大きなスケールの風に強く働きます。このような現象は、数値予報モデルの格子間隔で直接表現できるため、パラメタリゼーションは不要です。パラメタリゼーションは、格子より小さな現象を近似するための手法なので、 コリオリ力の計算には使われません。したがって、この記述は誤りです。

🌏 基本方程式とパラメタリゼーションの関係（簡潔に）

1. 基本方程式：モデルの“骨格”
数値予報モデルは、大気の運動やエネルギーのやりとりを記述する基本方程式に基づいています。主に以下のような方程式が使われます：

運動方程式（風の変化を表す）
連続の式（質量保存）
熱力学の式（温度変化）
状態方程式（気圧・温度・密度の関係）

これらは、格子点間隔で直接表現できるスケールの現象に対して、物理法則に基づいて厳密に計算されます。

2. パラメタリゼーション：モデルの“補助装置”
一方で、格子より小さなスケールの現象（例：雲の生成、降水、乱流、地表面との熱・水分交換など）は、基本方程式では直接扱えません。そこで登場するのがパラメタリゼーションです。

これは、小さなスケールの現象の平均的な影響を、格子点の物理量を使って近似的に表現する方法です。
たとえば：

雲や降水の生成 → 雲物理パラメタリゼーション
地表面との熱・水分交換 → 陸面過程スキーム
小規模な乱流 → 乱流パラメタリゼーション

🍃まとめると…

基本方程式は「直接計算できる現象」を扱い、

パラメタリゼーションは「直接計算できない小さな現象の影響」を補う役割を担っています。

まるで、基本方程式が大きな幹で、パラメタリゼーションがその枝葉のような存在。どちらもそろって、初めて「天気という森」が描けるんだね。

もっと詳しく図で整理したり、具体例を深掘りしたりもできるよ。どうする？🌦️📘

⑧数値予報モデルにおいて、「大気境界層の乱流による顕熱・潜熱の輸送量」は、パラメタリゼーションによって計算される。🟢

パラメタリゼーションとは、数値予報モデルの格子点間隔以下のスケールの現象による効果の見積もりのことです。つまり、数値予報モデルで計算される物理量が、パラメタリゼーションによって計算されるかどうかは、それに関わる現象が数値予報モデルの格子点間隔で直接表現できるかどうか、という点から判断できます。大気境界層では、地表面の摩擦や熱の影響を受けて乱流が卓越しており、乱流によって顕熱や潜熱が輸送されています。
乱流の渦の水平スケールは数cmから数百m なので、気象庁の数値予報モデルではそれらの渦を直接表現することはできません。したがって、大気境界層の乱流による顕熱・潜熱の輸送量は、パラメタリゼーションによって計算されますので、答えは正です。

⑨数値予報モデルにおいて、「格子スケールの上昇流による気温の断熱的な変化量」は、パラメタリゼーションによって計算される。

パラメタリゼーションとは、数値予報モデルの格子点間隔以下のスケールの現象による効果の見積もりのことです。つまり、数値予報モデルで計算される物理量が、パラメタリゼーションによって計算されるかどうかは、それに関わる現象が数値予報モデルの格子点間隔で直接表現できるかどうか、という点から判断できます。数値予報モデルの格子間隔で表現される気温が、上昇流によって断熱的に変化する過程は、その格子間隔で表現される上昇流から計算できます。
したがって、格子スケールの上昇流による気温の断熱的な変化量は、パラメタリゼーションで計算する必要はありませんので、答えは誤です。

⑩数値予報モデルにおいて、「水平方向の運動方程式に含まれる拡散・摩擦の効果」は、パラメタリゼーションによって計算される。

パラメタリゼーションとは、数値予報モデルの格子点間隔以下のスケールの現象による効果の見積もりのことです。
つまり、数値予報モデルで計算される物理量が、パラメタリゼーションによって計算されるかどうかは、それに関わる現象が数値予報モデルの格子点間隔で直接表現できるかどうか、という点から判断できます。
水平方向の運動方程式に含まれる拡散・摩擦の効果は、乱流拡散（局地的な風と大気安定度による運動量輸送）や地表面摩擦（地形・植生の影響による風の減速）といった格子スケール未満の物理過程であるため、気象庁の数値予報モデルでは直接表現することはできません。
したがって、水平方向の運動方程式に含まれる拡散・摩擦の効果は、パラメタリゼーションで計算する必要はありませんので、答えは誤です。

⑪数値予報モデルでは、連続的に変化する現実の大気の物理量を限られた数の格子点の値で代表しており、数値予報モデルで精度よく表現しうる現象は、水平スケールが格子間隔と同程度以上の現象である。

数値予報モデルとは、大気の変化をコンピューターでシミュレーションするためのプログラムです。
しかし、すべての場所のデータを細かく取ることはできないので、格子点という特定の地点でのデータを使います。ここで重要なのは、どれくらい細かくこの格子点を設定するかということです。
この間隔を格子間隔といいます。
では、気象現象の水平スケールと格子間隔の関係について考えてみましょう。
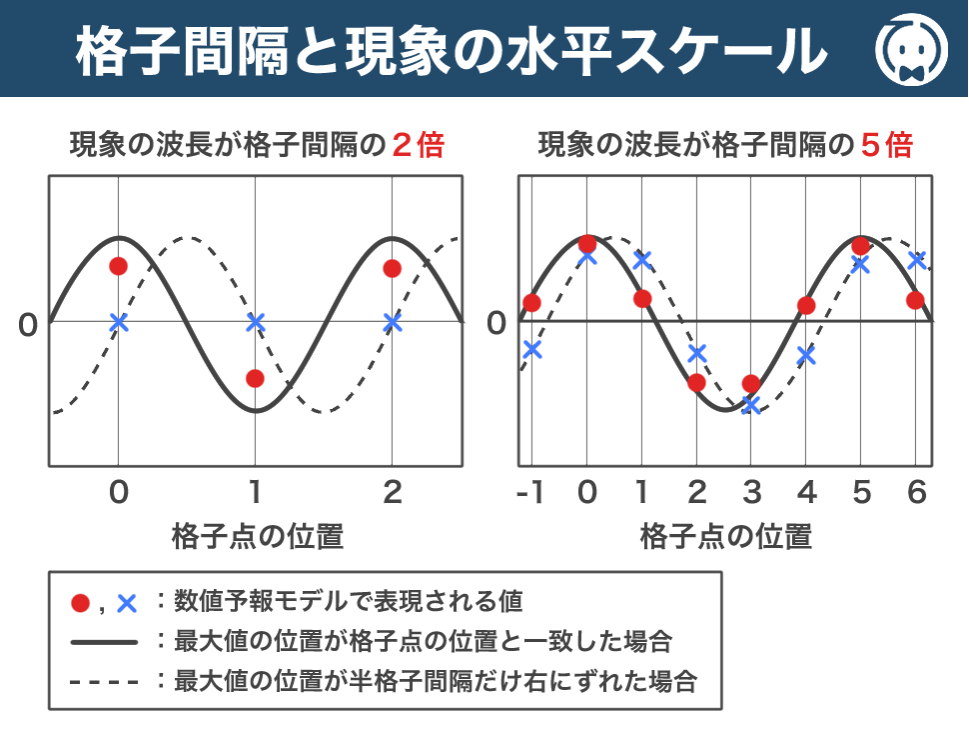
下図は、数値予報モデルの格子間隔と、現象の表現の関係を表しています。
左図は、現象の波長が格子間隔の２倍で、右図は、現象の波長が格子間隔の５倍となっています。
実線は、最大値の位置が格子点の位置と一致した場合を表し、破線は、半格子間隔だけ右にずれた場合を表しています。
● と ✕ は、それぞれ数値予報モデルで表現される値です。
（注意点として、数値予報モデルの格子点の値は格子スケールで平均化されているため、元の値より振幅が小さくなります。）
左図は、現象の波長が格子間隔よりそこまで大きくないので、振幅が大幅に過小評価されるだけでなく、現象の位置によっては全く表現されないこともあり得ます。
一方、右図は、現象の波長が格子間隔より大きいので、現象の位置に関係なく比較的正確に表現されています。
これらの図は、現象の水平スケールが格子間隔よりある程度大きくないと、その現象を正しく表現できないことを表しています。
例えば、全球モデル（GSM）は格子間隔が約13kmですが、それより小さい波長（例：５kmや10km）の現象はこのモデルではうまく表現できません。
一方、波長が100kmくらい大きなスケールの現象は、比較的正確に表現されます。
経験的には、数値予報モデルが精度よく表現できる現象の水平スケールは、数値予報モデルの格子間隔の５～８倍以上とされています。
したがって、数値予報モデルで精度よく表現しうる現象は、「水平スケールが格子間隔と同程度以上の現象」ではなく、「格子間隔の５～８倍以上」とされていますので、答えは誤です。

⑫積乱雲のような水平スケールが概ね10km以下の現象を予測するため、メソモデルや局地モデルでは非静力学方程式系を採用しており、これらのモデルでは、鉛直流を質量保存則の式から診断的に計算している。

非静力学方程式系とは、積乱雲や積乱雲群のような、鉛直スケールに比べて水平スケールが十分大きいとはいえない現象を予測するための手法で、メソモデル（MSM）や局地モデル（LFM）などで採用されています。
この方程式系には鉛直流の予報方程式があり、鉛直流はその方程式を時間積分することで求めています。
一方、鉛直流を質量保存則の式から診断的に計算しているのは、全球モデル（GSM）などで採用されているプリミティブ方程式系です。
プリミティブ方程式系では、鉛直流の予報方程式が静力学平衡の式に置き換えられているため、静力学平衡の式から直接的に鉛直流を求めることはできません。
しかし、静力学近似を適用すると、質量保存則の式には時間変化の項が含まれなくなります。
これを利用することで、鉛直流を質量保存則の式から水平風の予測値から診断的に計算しています。
したがって、メソモデル（MSM）や局地モデル（LFM）では「鉛直流は質量保存則の式から診断的に計算している」のではなく、「非静力学方程式系の鉛直流の予報方程式を時間積分して鉛直流を計算しています」ので、答えは誤です。

⑬数値予報モデルでは、格子点の物理量で表現した大気の状態を、一定の時間間隔（時間ステップ）で計算を繰り返して将来の大気の状態を予測する。時間ステップを大きくすると計算時間を短縮できるが、ある上限をこえると計算が不安定になり、物理的に意味をなさない値が出力されたり、計算が続けられなくなったりする。

数値予報モデルでは、格子点の物理量で表現した大気の状態を、一定の時間間隔（時間ステップ）で計算を繰り返して将来の大気の状態を予測します。
例えば、全球モデル（GSM）では400秒（６分40秒）、メソモデル（MSM）では20秒、局地モデル（LFM）では８秒ごとに計算を繰り返しています。
しかし、この時間ステップが大きすぎると、計算と計算の間に大気の状態が変化しすぎてしまい、正しい計算ができなくなってしまいます。
これを防ぐためには、時間ステップが、空気の流れの速さ（＝風速など）や、格子点間隔に対して、小さすぎないようにしなければなりません。
この条件のことを CFL条件（または、クーラン条件）といいます。
（CFLという名前は、この条件を提唱したクーラン、フリードリヒ、ルーウィーの３人の名前の頭文字から取ったものです。）
CFL条件は Δ𝑥 を格子点間隔、 Δ𝑡 を時間ステップ、 𝐶 を流れの速さとすると、以下の式で表されます。

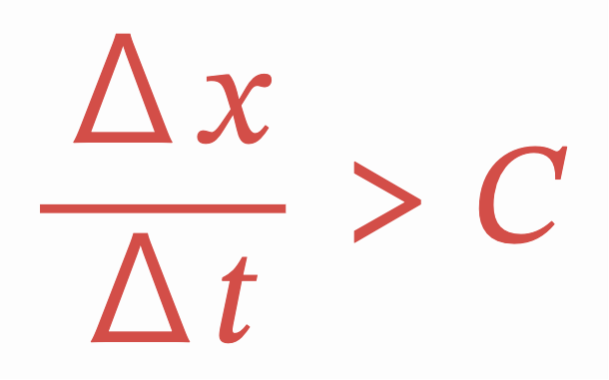
この式は、数値予報モデルで安定した計算を行うためには、Δ𝑥/Δ𝑡 が 𝐶 よりも大きくなければならない、ということを意味しています。
例えば、格子間隔が Δx = 20km で、風速が C = 50m/s である場合を考えてみます。
Δt を求めるために、CFL条件の「>」を「=」に変えて計算してみると
Δt = Δx / C = 20000[m] / 50[m/s] = 400[s]
となります。
つまり、この場合の時間ステップの上限は 400秒となり、これより大きな時間ステップ（500秒や600秒など）では、計算が安定しないということが分かります。
ちなみに、全球モデル（GSM）は2023年３月に格子点間隔が約20kmから約13kmに変更されました。
上記のCFLで計算すると、Δt = Δx / C = 13000[m] / 50[m/s] = 260[s] となり、理論上の時間ステップは約260秒となりますが、現在も格子点間隔が約20kmのときの時間ステップである400秒で計算しています。
また、実際の大気はそのときどきで風速が異なるため、今回のように 50m/s と常に同じというわけではありませんが、その都度、時間ステップは変えませんので、風速が大きいなど最も厳しい気象条件を想定してあてはめることになります。
そのような理由から、ここでは風速を 50m/s にし、厳しい条件を想定して考えています。
したがって、数値予報モデルでは、時間ステップがある上限をこえると計算が不安定になり、物理的に意味をなさない値が出力されたり、計算が続けられなくなったりしますので、答えは正です。

⑭数値予報は、過去の観測値と気象現象との関係の統計的資料に基づいて、将来の気象現象をコンピュータでシミュレーションする手法である。誤

数値予報とは、計算機（コンピューター）を用いて地球大気や海洋・陸地の状態の変化を数値シミュレーションによって予測するものです。
具体的には、最初に地球大気や海洋・陸地を細かい格子に分割し、世界から送られてくる観測データに基づいて、それぞれの格子にある時刻の気温・風などの気象要素や海面水温・地面温度などの値を割り当てます。
次にこうして求めた「今」の状態から、運動方程式や、熱力学方程式、質量保存の式などの物理学や化学の法則に基づいてそれぞれの値の時間変化を計算することで「将来」の状態を予測します。
この計算に用いるコンピュータープログラムを「数値予報モデル」といいます。
したがって、数値予報は、「過去の観測値と気象現象との関係の統計的資料」ではなく「現在の観測値と大気の物理学や化学の法則」に基づいて、将来の気象現象をコンピュータでシミュレーションする手法ですので、答えは誤です。

⑮数値予報では、大気中に３次元の格子を設定し、各格子点には、その格子点に最も近い観測地点における観測データを与え、これに方程式を当てはめて計算する。

数値予報で各格子点にデータを与える方法は、データ同化という手法が用いられています。
これは、周囲の観測データと前回の予測値を組み合わせて、格子点ごとの大気の状態を推定する手法です。
具体的な手順は次の通りです。
① 観測データの収集と品質管理
地上観測、ラジオゾンデ、航空機、衛星などによって得られた観測データのうち、品質管理によって誤差の大きいデータを除外または補正します。
② 第一推定値の作成
前回の数値予報モデルの結果をもとにした現在の予測値（＝第一推定値）を作成します。
③ 観測データと第一推定値の統合
観測データと第一推定値を統計的手法で統合し、解析値を作成します。
④ 解析値の格子点への割り当て
得られた解析値を、数値予報モデルの３次元格子点に割り当て、初期条件として使用します。
したがって、数値予報の各格子点には「格子点に最も近い観測地点における観測データ」ではなく「格子点周囲の複数の観測地点のデータと第一推定値を統計的に処理したデータ」を与え、これに方程式を当てはめて計算しますので、答えは誤です。

⑯数値予報モデルとは、大気の状態の変化を物理学の方程式に従って計算する手順を定めたものである。

数値予報モデルとは、コンピューターを用いて大気や海洋、陸地の状態変化を数値的にシミュレーションし、将来の気象状態を予測するための計算プログラムのことです。
大気の状態変化を求める計算プログラムとしては、格子点値で表現して計算する格子モデルや、関数の重ね合わせで表現して計算するスペクトルモデルがあります。
（「スペクトルモデル」という表現には、「見える形で現れる波の成分」というニュアンスが込められている。したがって、答えは正です。

⑰気象庁では地球全体をカバーする全球モデルによって数日先の大気の状態を予想している。

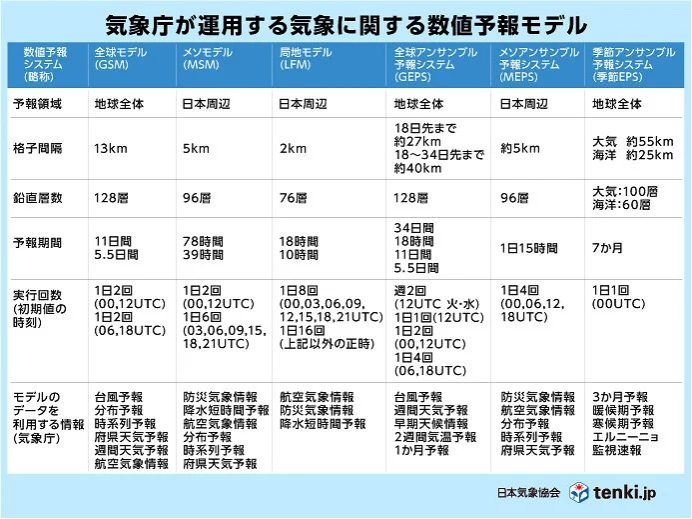
全球モデル（GSM）とは、地球全体を対象とする気象庁の数値予報モデルで、水平スケールが 100km 以上の総観スケール（大規模）現象の予測を目的としています。
水平格子間隔（水平分解能）は約13km、鉛直方向は 128層です。
したがって、答えは正です。

⑱気象庁のメソモデルは、全球モデルでは予測できないメソ気象現象を予測するための数値予報モデルである。

メソモデル（MSM）とは、日本とその近海を対象とする気象庁の数値予報モデルで、水平スケールが数10km 程度以上のメソスケール（中規模）現象の予測を目的としています。水平格子間隔（水平分解能）は５km、鉛直方向は 96層です。したがって、答えは正です。

⑲気象庁の全球モデルは、高・低気圧、梅雨前線、台風など、水平スケールが100km以上の現象を予測し、週間天気予報などに利用されている。

全球モデル（GSM）は、水平スケールが 100km以上の現象を予測しています。　　
具体的には、高・低気圧、梅雨前線、台風などの大規模現象を予測しており、週間天気予報、府県天気予報、台風予報などに利用されています。したがって、答えは正です。

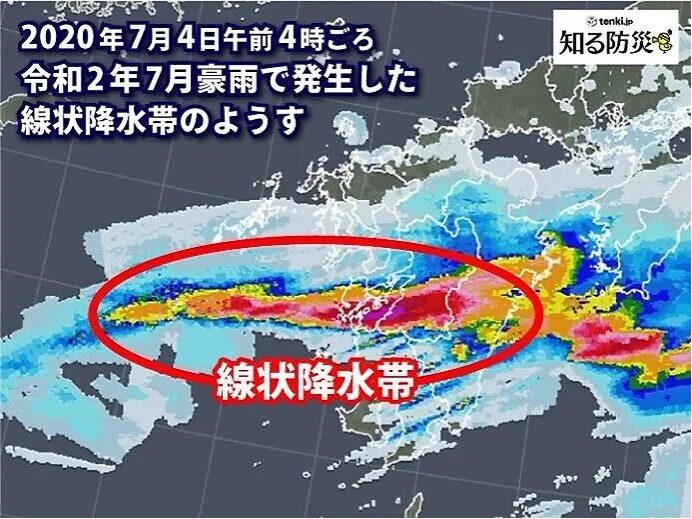
⑳気象庁のメソモデルは、全球モデルよりも水平解像度が高いとはいえ、線状降水帯を予測することはできない。

数値予報モデルが表現できる現象の水平スケールは、水平格子間隔の５～８倍以上とされています。
そのため、長さ 50～300km 程度、幅 20〜50km 程度の線状降水帯は、水平格子間隔が５km のメソモデルで予測することが可能です。
したがって、気象庁のメソモデルは、線状降水帯を予測することは「できない」ではなく「できます」ので、答えは誤です。

㉑個々の積乱雲の振る舞いについては、格子間隔が２kmの局地モデルで精度良く表現することができる。

数値予報モデルが表現できる現象の水平スケールは、水平格子間隔の５～８倍以上とされています。
そのため、水平スケールが数100m～数km の個々の積乱雲の振る舞い（発生・発達・衰弱など）は、水平格子間隔が２km の局地モデルでも精度良く表現することはできません。したがって、答えは誤です。

㉒メソモデルでは、領域外の情報を得るために全球モデルの予測結果を使っているため、全球モデルに予測誤差がある場合、メソモデルの予測はその誤差の影響を受ける。

メソモデルの計算領域は、日本とその近海であるため、領域の外側（境界部分）の気象データは側面境界値として全球モデルから受け取ります。
つまり、メソモデルの予測には、全球モデルの予測結果も用いられているため、全球モデルに予測誤差があれば、メソモデルもその影響を受けます。
したがって、答えは正です。

㉓重力波ノイズは、風と気圧場がバランスしていないときに、予報計算の終盤に発生しやすいので、長時間の予報計算の安定性を損なうことはない。

重力波ノイズは、風と気圧場のバランスが崩れたときに発生する短周期の波動で、予報計算の初期に現れやすいという特徴があります。例えば、山岳地帯で風が乱れたり、前線の急激な変化が起きたりするときに、小さな気圧の波が立ち上がるイメージです。このノイズは計算の初期段階で増幅しやすいため、そのまま放置すると長時間の予報計算の安定性が損なわれてしまいます。
したがって、重力波ノイズは、長時間の予報計算の安定性を「損ないます」ので、答えは誤です。

㉔第一推定値は、数値予報モデルにおいて、初期時刻から最初の微小時間後の予測値のことを指す。

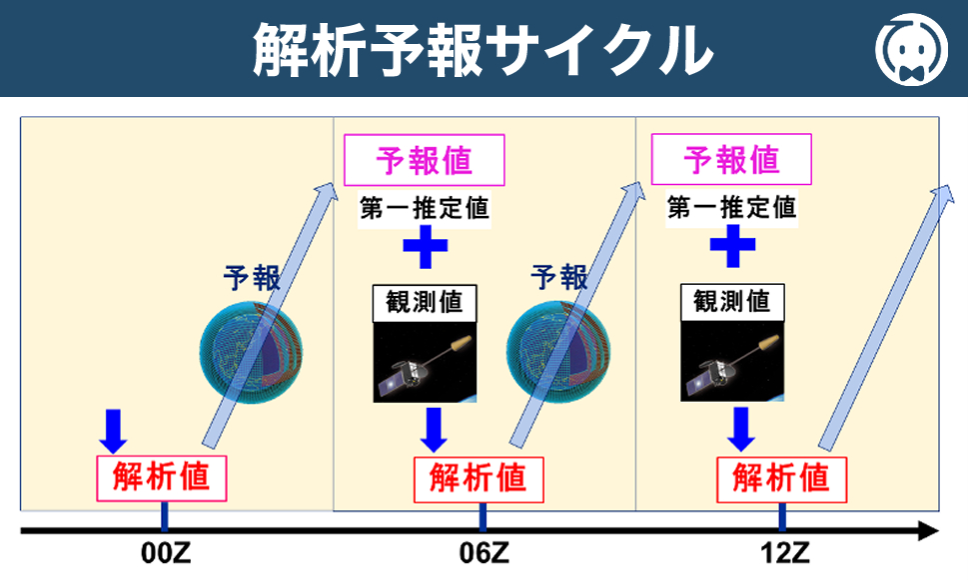
第一推定値とは、解析対象時刻より前の時刻を初期時刻として、数値予報モデルで得られた現在時刻についての予測値のことで、観測データとともに客観解析に用いる格子点値です。
数値予報では、一定の時間間隔（例：6時間ごと）でデータ同化と予報を繰り返す解析予報サイクルが行われています。このサイクルでは、前回の解析値を初期条件として予報を行い、その結果を第一推定値として次の解析に利用することで、観測データが乏しい地域や時刻でも、全格子点における大気の計算が可能となります。
したがって、第一推定値は、数値予報モデルにおいて、「初期時刻から最初の微小時間後の予測数値」ではなく「解析対象時刻より前の時刻を初期時刻として、数値予報モデルで得られた現在時刻についての予測値」のことを指しますので、答えは誤です。

㉕局地モデルの予報結果が受ける局地モデルの予報領域の境界で取り込むメソモデルの予測の影響は、予報時間が短いほど大きく、長いほど小さくなる。

局地モデルの計算領域は、日本全域であるため、領域の外側（境界部分）の気象データは側面境界値としてメソモデルから受け取ります。
つまり、局地モデルの予測には、メソモデルの予測結果も用いられているため、メソモデルに予測誤差があれば、局地モデルもその影響を受けます。
そしてその影響は、予報時間が短いほど小さく、長いほど大きくなります。
したがって、局地モデルの予報領域の境界で取り込むメソモデルの予測の影響は、予報時間が短いほど「大きく」ではなく「小さく」、長いほど「小さく」ではなく「大きく」なりますので、答えは誤です。

㉖客観解析では、予報値と観測値のそれぞれに見込まれる誤差の大きさは考慮せず、格子点ごとに最適な値を求めている。

第一推定値である数値予報モデルの予報値を観測データで修正し、大気の初期値を求める処理を客観解析（データ同化）といいます。
客観解析では、予報値と観測データのそれぞれに見込まれる誤差の大きさを考慮して、格子点ごとに最適な値が求められています。
したがって、客観解析では、予報値と観測値のそれぞれに見込まれる誤差の大きさを「考慮せず」ではなく「考慮して」、格子点ごとに最適な値を求めていますので、答えは誤です。

㉗数値予報モデルの格子間隔を狭めて水平解像度を高めると、地形や海陸の分布をより現実に近く表現できるので、地形性の降水現象などの予報精度は向上する。

水平解像度が高くなると山脈などの地形をより現実に近く表現できるので、山脈の風上側斜面で降る地形性の雨の予報精度は向上します。したがって、答えは正です。

㉘数値予報モデルにおける格子間隔、大気の流れの速さ、時間ステップの間には、「格子間隔 / 時間ステップ＜大気の流れの速さ」の関係を満たさなければならないという条件がある。

数値予報モデルでは、一定時間（時間ステップ）ごとに大気の状態の計算を繰り返して未来の状態を予測します。
この計算を安定させるには、計算のタイミング（時間ステップ）を、現象の伝わるスピードより速くしないことが大切です。
より専門的に言うと、「格子間隔 / 時間ステップ＞大気の流れの速さ」の関係を満たす必要があるとされています。
この条件を CFL条件といいます。
（CFL条件という名前は、1928年にこの条件を提唱した３人の数学者 Courant（リヒャルト・クーラント）、Friedrichs（カート・フリードリヒ）、Lewy（ハンス・レヴィー）の頭文字に由来しています。）
したがって、数値予報モデルでは「格子間隔 / 時間ステップ＜大気の流れの速さ」ではなく「格子間隔 / 時間ステップ＞大気の流れの速さ」の関係を満たさなければならないというCFL条件がありますので、答えは誤です。

㉙気象庁の全球モデルでは、鉛直方向の運動方程式は、重力と鉛直方向の気圧傾度力が釣り合っていると仮定し、静力学平衡の式を用いている。

全球モデルでは、予報対象の現象の鉛直スケールは水平スケールよりもはるかに小さいので、「鉛直方向の気圧傾度力＝重力加速度」と仮定し、鉛直方向の運動方程式には静力学平衡（静水圧平衡）の式を用いています。
また、静力学平衡近似（静力学平衡の仮定）を用いた数値予報モデルをプリミティブモデルといいます。
したがって、気象庁の全球モデルでは、鉛直方向の運動方程式は、重力と鉛直方向の気圧傾度力が釣り合っていると仮定し、静力学平衡の式を用いていますので、答えは正です。

㉚気象庁では、数時間先から１日先の大雨や暴風雨などの災害をもたらす現象の予報には、非静力学モデルであるメソモデルを使用し、週間天気予報にはプリミティブモデルである全球モデルを使用している。

メソモデルは、非静力学モデルを使用しており、数時間先から１日先の大雨や暴風雨などの災害をもたらす現象の予報などに利用されています。
非静力学モデルでは、大気の鉛直方向の運動（上昇流や対流）を静力学平衡とせず、運動方程式を用いて直接計算します。
このため、水平格子間隔が５km のメソモデルは、活発な対流や局地的で激しい気象現象の予報を行うのに適しています。
一方、全球モデルは、静力学モデル（プリミティブモデル）を使用しており、週間天気予報などに利用されています。
静力学モデルでは、大気の鉛直方向の気圧傾度力と重力が釣り合っている（静力学平衡）という近似を用います。
このため、水平格子間隔が約13km の全球モデルは、広い範囲で緩やかに変化する現象（高・低気圧や台風、梅雨前線など）の予報を行うのに適しています。
したがって、気象庁では、数時間先から１日先の大雨や暴風雨などの災害をもたらす現象の予報には、非静力学モデルであるメソモデルを使用し、週間天気予報にはプリミティブモデルである全球モデルを使用していますので、答えは正です。

㉛４次元変分法による解析では、数値予報モデルを実行することで大気状態の時間変化を考慮するため、３次元変分法による解析に比べて計算量が多くなる。

３次元変分法とは、大気状態の時間変化を考慮せず立体空間の３次元を解析する手法です。
４次元変分法とは、立体空間の３次元に時間を加えた４次元で大気の状態を捉えることで、より高精度な解析値が得られる手法です。
そのため、４次元変分法による解析では、3次元変分法による解析に比べて計算量が多くなりますので、答えは正です。

㉜数値予報モデルで表現可能な大気現象の最小水平スケールは、格子間隔までである。

数値予報モデルで表現可能な最小スケールは、「格子間隔まで」ではなく「格子間隔の５～８倍」ですので、答えは誤です。

㉝全球モデルの初期値を作成する全球解析の４次元変分法には、アンサンブル予報から見積もられる予報誤差を組み込んだハイブリッドデータ同化手法が用いられている。

全球モデルの初期値を作成するための全球解析では、４次元変分法が使われています。
４次元変分法とは、立体空間の３次元に時間を加えた４次元で大気の状態を捉えることで、より高精度な解析値が得られる手法です。
この手法は、過去の統計から得られた平均的な予報誤差を使用しているため、実際の天気の状況によって誤差の大きさや分布変わってしまうという問題点がありました。
そこで、アンサンブル予報という複数の予報を同時に行う手法から、その時々の予報誤差を見積もり、それを４次元変分法に組み込むハイブリッドデータ同化という手法が導入されました。
この手法により、大気の状態をより正確に把握でき、結果として天気予報の精度が向上しています。
したがって、全球モデルの初期値を作成する全球解析の４次元変分法には、アンサンブル予報から見積もられる予報誤差を組み込んだハイブリッドデータ同化手法が用いられていますので、答えは正です。

㉞全球解析、メソ解析及び局地解析に取り込まれる観測データには、同じ解析対象時刻・同じ領域で比べても、違いがある。その理由の一つは、各客観解析によって、解析対象時刻から計算処理を開始するまでの時間が異なることである。

全球解析、メソ解析、局地解析では、同じ解析対象時刻や同じ領域であっても取り込まれる観測データに違いが生じます。
これは、解析対象時刻から計算処理を開始するまでの時間がそれぞれ異なるためです。
全球解析では世界中の観測データを集める必要があるため、解析対象時刻から計算開始までに約２時間20分かかります。
一方、メソ解析は約50分、局地解析は約30分と、より短時間で処理を始めます。
この時間差により、全球解析はより多くの観測データを取り込めるのに対し、局地解析は速報性を優先して一部の観測データが使えないことがあります。
したがって、全球解析、メソ解析及び局地解析に取り込まれる観測データには、同じ解析対象時刻・同じ領域で比べても違いがあり、その理由の一つは、各客観解析によって、解析対象時刻から計算処理を開始するまでの時間が異なることですので、答えは正です。